I have been traveling to conferences and getting out publications, so have not been posting my planned “Tit for Tat, It Ain’t All That” series as quickly as I intended.  But here is Part 1:

Many readers of this blog will be familiar with the Prisoner’s Dilemma.  In case you are looking for a refresher, Zach Weinersmith has an SMBC comic with a pretty good summary of the usual set up.

In this series of posts I am going to use the formulation of the 2-player Prisoner’s Dilemma commonly used by biologists. One advantage of the biologists’ formulation is that the choices and payoffs are easier to remember (at least for me)  than the list of years a prisoner might get for confessing or not.  Another is that it only has two terms, which makes it more easy to work with mathematically. The disadvantage is that it is not as general as the standard economists formulation (by this I mean that there are 2-player Prisoner’s Dilemmas that cannot be expressed in the biologists’ formulation), but for our purposes in these blog posts we will be able to capture the complexity we need.

In the biologists’ formulation, you (let’s pretend that you are playing the game) are paired with another player and can give that player a gift.  The gift gives them a benefit of size b. However, giving the gift costs you.  The amount it costs you is c. Meanwhile and simultaneously, the other player is deciding whether to give you a gift that will benefit you by b and cost them c. We will call giving a gift “cooperation” and not giving a gift “defection.”

The below matrix shows the payoffs to the row player. As in Zach’s comic, your highest payoff is to defect, no matter what the other player does. In addition, the other player’s highest payoff is also to defect. However, as long as b > c, you would have both been better off had you both cooperated. Hence, the dilemma.

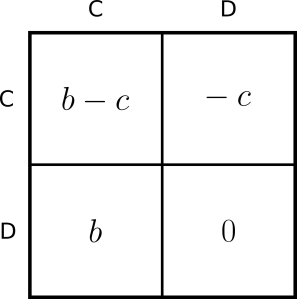
The “rational solution” to the 2-player Prisoner’s Dilemma is well known.  Both players tragically defect.

But what if we add a twist where both players might meet again? If players play the game repeatedly, the thought is, perhaps cooperating in earlier interactions would encourage the other player to cooperate in later interactions, in the long-run, both players will  “escape” the dilemma by harvesting the rewards of repeated cooperation. This is a fairly seductive idea and is, in my experience, the thought to be the primary mechanism for escaping the Prisoner’s Dilemma in economics and, especially, political science.

However, in this series of blog posts, I plan to show that repeated interactions are not the panacea for solving the problems of cooperation that many think it is. The real story is a little more complicated and, frankly, a ton more interesting!